Category: Visualizations

For a recent research project on discrete spacetimes, I have been using finite element methods to solve the Helmholtz equation on various interesting 2-dimensional triangulated manifolds. A little while ago, I realized that a neat by-product of these calculations is the ability to easily solve the free particle Schrodinger equations in these geometries. In the physics literature, this problem is sometimes called “quantum billiards” because it is the quantum mechanical analogue of studying the motion of billiard balls (on oddly shaped tables).

Here is an example:

This movie shows the position probability density of a free particle confined to an elliptical cavity (i.e. the modulus squared of the position space wavefunction). Here is a version of the same movie with the trajectory of a classical particle with the same initial position and velocity as the quantum wavepacket superimposed:

At the initial time, the particle is localized near the centre of the ellipse and has a velocity directed up and to the right. The particle’s wavepacket scatters off the walls of the ellipse several times. Each collision caused the wavepacket to spread out in space, and, by the end of the movie, the particle is de-localized over most of the ellipse. Interference patterns are formed as portions of the reflected wavefunction from different collisions interact with one another.

In the above movie, you should be able to see that the ellipse is actually made up of a bunch of small coloured triangles. This is because I am not actually solving the Schrodinger equation within a continuous elliptical region, I am rather solving for a discrete version of the wave function defined on a triangulation of the ellipse. By making the triangles smaller one gets a better and better approximation to the continuous case. But the catch is that as the triangles get smaller, the computational time to generate the movies gets longer. The movies on this page are the result of simulations that take a few hours on my laptop.

Here is another movie in a related geometry, the Bunimovich Stadium:

The Bunimovich Stadium is essentially a rectangle with semi-circular caps. It is interesting because a classical particle contained within it exhibits ergodicity. That is, if you consider a classical billiard ball in this region with a random initial position and velocity, is trajectory will (almost always) eventually fill up the entire stadium uniformly. The above simulation is possibly hinting at the quantum analogue of this classical ergodicity, with the final wavefunction configuration being even more dispersed than the elliptical case.

The next example I looked at was meant to be similar to the famous double slit experiment:

In this movie, the particle lives in a circular arena with a triangular obstacle in the middle. The obstacle cleaves the particle’s wavefunction in two, essentially meaning that there is an equal probability of measuring the particle taking a path above or below the triangle. After the splitting, we can see the development of intricate interference patterns, just like in the double slit experiment.

Here is another example of a wavepacket interacting with a 2-dimensional barrier:

In this case, the particle undergoes a glancing collision with a circular obstacle in a hexagonal arena.

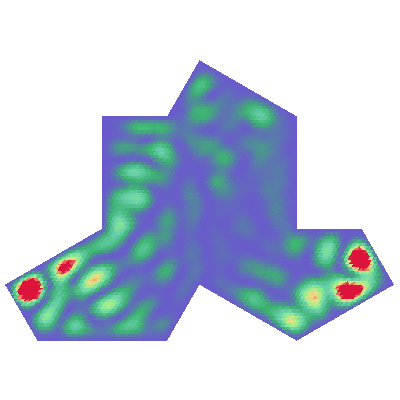
Finally, this movie shows a quantum particle confined to the newly discovered aperiodic monotile:

The aperiodic monotile has a remarkable property: it can be used to tile a 2-dimensional plane in a completely non-repeating way. It is pretty unclear to me how the tiling properties of the monotile might relate to the trajectory of confined quantum particles, but it does make for a pretty movie…

Several years ago (for reasons that I can’t really remember) I became interested in 4-dimensional polyhedra. I made some animations that I like looking at, and I wanted to try out my new blog, so here we are…

4-dimensional polyhedra are the higher dimensional generalizations of three dimensional objects such cubes and tetrahedrons. You can think of them as solid objects that are highly symmetric; that is, their edges all have the same length, their faces are all congruent, and the angles at all of their vertices are the same. A familiar 3-dimensional example is a cube whose consists of six identical 2-dimensional regions, each of which is a square. The 4-dimensional version of cube is called a tesseract (or 8-cell). It’s boundary consists of 8 identical 3-dimensional regions, each of which is a cube.

How can you visualize a 4-dimensional object? Well, strictly speaking this is not something that human ought to be able to do, since our brains are trained to operate in a 3-dimensional world. But we can play a simple trick to draw pictures of 4 dimensional polyhedra by looking at their shadows. In the real world, the shadow of 3-dimensional object on a wall is 2-dimensional, and can therefore be accurately represented on a piece of paper. So, it is therefore possible to represent a 4-dimensional object by imagining what its shadow would look like on a 3-dimensional “screen”.

That’s exactly what the animated gifs shown below demonstrate: a 3-dimensional rendering of the shadow of several examples of these objects. Each of the polyhedra is rotating in 4-dimensional space.

In order, the polyhedra depicted are the 5-cell (two views), the 8-cell (two views), the 16 cell, the 24 cell, and the 120 cell. The animations were prepared using Maple.